Wallet provider blockchain partners with indian bitcoin exchangecoindesk
50 comments
Where to buy bar keepers friend liquid cleanser limpiador
RSA Rivest—Shamir—Adleman is one of the first public-key cryptosystems and is widely used for secure data transmission. In such a cryptosystem , the encryption key is public and it is different from the decryption key which is kept secret private. In RSA, this asymmetry is based on the practical difficulty of the factorization of the product of two large prime numbers , the " factoring problem ". Clifford Cocks , an English mathematician working for the British intelligence agency Government Communications Headquarters GCHQ , had developed an equivalent system in , but this was not declassified until A user of RSA creates and then publishes a public key based on two large prime numbers , along with an auxiliary value.
The prime numbers must be kept secret. Anyone can use the public key to encrypt a message, but with currently published methods, and if the public key is large enough, only someone with knowledge of the prime numbers can decode the message feasibly. Whether it is as difficult as the factoring problem remains an open question. RSA is a relatively slow algorithm, and because of this, it is less commonly used to directly encrypt user data.
More often, RSA passes encrypted shared keys for symmetric key cryptography which in turn can perform bulk encryption-decryption operations at much higher speed.
The idea of an asymmetric public-private key cryptosystem is attributed to Whitfield Diffie and Martin Hellman , who published this concept in They also introduced digital signatures and attempted to apply number theory.
Their formulation used a shared-secret-key created from exponentiation of some number, modulo a prime number. However, they left open the problem of realizing a one-way function, possibly because the difficulty of factoring was not well-studied at the time.
Ron Rivest , Adi Shamir , and Leonard Adleman at the Massachusetts Institute of Technology made several attempts, over the course of a year, to create a one-way function that was hard to invert. Rivest and Shamir, as computer scientists, proposed many potential functions, while Adleman, as a mathematician, was responsible for finding their weaknesses. They tried many approaches including " knapsack -based" and "permutation polynomials".
For a time, they thought what they wanted to achieve was impossible due to contradictory requirements. He spent the rest of the night formalizing his idea, and he had much of the paper ready by daybreak. The algorithm is now known as RSA — the initials of their surnames in same order as their paper. Clifford Cocks , an English mathematician working for the British intelligence agency Government Communications Headquarters GCHQ , described an equivalent system in an internal document in His discovery, however, was not revealed until due to its top-secret classification.
MIT was granted U. Patent 4,, for a "Cryptographic communications system and method" that used the algorithm, on September 20, Though the patent was going to expire on September 21, the term of patent was 17 years at the time , the algorithm was released to the public domain by RSA Security on September 6, , two weeks earlier.
Had Cocks's work been publicly known, a patent in the United States would not have been legal either. From the DWPI 's abstract of the patent,. The system includes a communications channel coupled to at least one terminal having an encoding device and to at least one terminal having a decoding device. A message-to-be-transferred is enciphered to ciphertext at the encoding terminal by encoding the message as a number M in a predetermined set. That number is then raised to a first predetermined power associated with the intended receiver and finally computed.
The remainder or residue, C, is The RSA algorithm involves four steps: In addition, for some operations it is convenient that the order of the two exponentiations can be changed and that this relation also implies:.
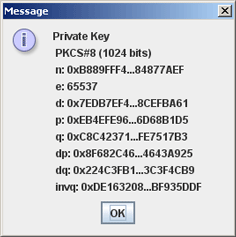
RSA involves a public key and a private key. The public key can be known by everyone, and it is used for encrypting messages. The intention is that messages encrypted with the public key can only be decrypted in a reasonable amount of time by using the private key. The public key is represented by the integers n and e ; and, the private key, by the integer d although n is also used during the decryption process. Thus, it might be considered to be a part of the private key, too.
The public key consists of the modulus n and the public or encryption exponent e. The private key consists of the private or decryption exponent d , which must be kept secret. That the Euler totient function can be used can also seen as consequence of the Lagrange's theorem applied to the multiplicative group of integers modulo pq.
Since it is beneficial to use a small value for e e. Suppose that Bob wants to send information to Alice. If they decide to use RSA, Bob must know Alice's public key to encrypt the message and Alice must use her private key to decrypt the message.
To enable Bob to send his encrypted messages, Alice transmits her public key n , e to Bob via a reliable, but not necessarily secret, route. Alice's private key d is never distributed. After Bob obtains Alice's public key, he can send a message M to Alice. He then computes the ciphertext c , using Alice's public key e , corresponding to.
This can be done reasonably quickly, even for bit numbers, using modular exponentiation. Bob then transmits c to Alice.
Alice can recover m from c by using her private key exponent d by computing. Given m , she can recover the original message M by reversing the padding scheme. Here is an example of RSA encryption and decryption. The parameters used here are artificially small, but one can also use OpenSSL to generate and examine a real keypair. For a padded plaintext message m , the encryption function is. For an encrypted ciphertext c , the decryption function is.
Both of these calculations can be computed efficiently using the square-and-multiply algorithm for modular exponentiation. In real-life situations the primes selected would be much larger; in our example it would be trivial to factor n , obtained from the freely available public key back to the primes p and q. Practical implementations use the Chinese remainder theorem to speed up the calculation using modulus of factors mod pq using mod p and mod q.
The values d p , d q and q inv , which are part of the private key are computed as follows:. Here is how d p , d q and q inv are used for efficient decryption. Encryption is efficient by choice of a suitable d and e pair. A working example in JavaScript using BigInteger. This code should not be used in production, as bigInt. Suppose Alice uses Bob 's public key to send him an encrypted message. In the message, she can claim to be Alice but Bob has no way of verifying that the message was actually from Alice since anyone can use Bob's public key to send him encrypted messages.
In order to verify the origin of a message, RSA can also be used to sign a message. Suppose Alice wishes to send a signed message to Bob. She can use her own private key to do so. She produces a hash value of the message, raises it to the power of d modulo n as she does when decrypting a message , and attaches it as a "signature" to the message.
When Bob receives the signed message, he uses the same hash algorithm in conjunction with Alice's public key. He raises the signature to the power of e modulo n as he does when encrypting a message , and compares the resulting hash value with the message's actual hash value.
If the two agree, he knows that the author of the message was in possession of Alice's private key, and that the message has not been tampered with since. Although the original paper of Rivest, Shamir, and Adleman used Fermat's little theorem to explain why RSA works, it is common to find proofs that rely instead on Euler's theorem. Assuming that m is relatively prime to n , we have. When m is not relatively prime to n , the argument just given is invalid. To avoid these problems, practical RSA implementations typically embed some form of structured, randomized padding into the value m before encrypting it.
This padding ensures that m does not fall into the range of insecure plaintexts, and that a given message, once padded, will encrypt to one of a large number of different possible ciphertexts. Because these schemes pad the plaintext m with some number of additional bits, the size of the un-padded message M must be somewhat smaller. RSA padding schemes must be carefully designed so as to prevent sophisticated attacks which may be facilitated by a predictable message structure.
Early versions of the PKCS 1 standard up to version 1. However, at Crypto , Bleichenbacher showed that this version is vulnerable to a practical adaptive chosen ciphertext attack. Furthermore, at Eurocrypt , Coron et al.
Secure padding schemes such as RSA-PSS are as essential for the security of message signing as they are for message encryption. Use of PSS no longer seems to be encumbered by patents. Note that using different RSA key-pairs for encryption and signing is potentially more secure. NET use the following optimization for decryption and signing based on the Chinese remainder theorem. The following values are precomputed and stored as part of the private key:. This is more efficient than computing exponentiation by squaring even though two modular exponentiations have to be computed.
The reason is that these two modular exponentiations both use a smaller exponent and a smaller modulus. The security of the RSA cryptosystem is based on two mathematical problems: Full decryption of an RSA ciphertext is thought to be infeasible on the assumption that both of these problems are hard, i. Providing security against partial decryption may require the addition of a secure padding scheme.
The RSA problem is defined as the task of taking e th roots modulo a composite n: Currently the most promising approach to solving the RSA problem is to factor the modulus n. With the ability to recover prime factors, an attacker can compute the secret exponent d from a public key n , e , then decrypt c using the standard procedure. No polynomial-time method for factoring large integers on a classical computer has yet been found, but it has not been proven that none exists.
See integer factorization for a discussion of this problem. Multiple polynomial quadratic sieve MPQS can be used to factor the public modulus n.