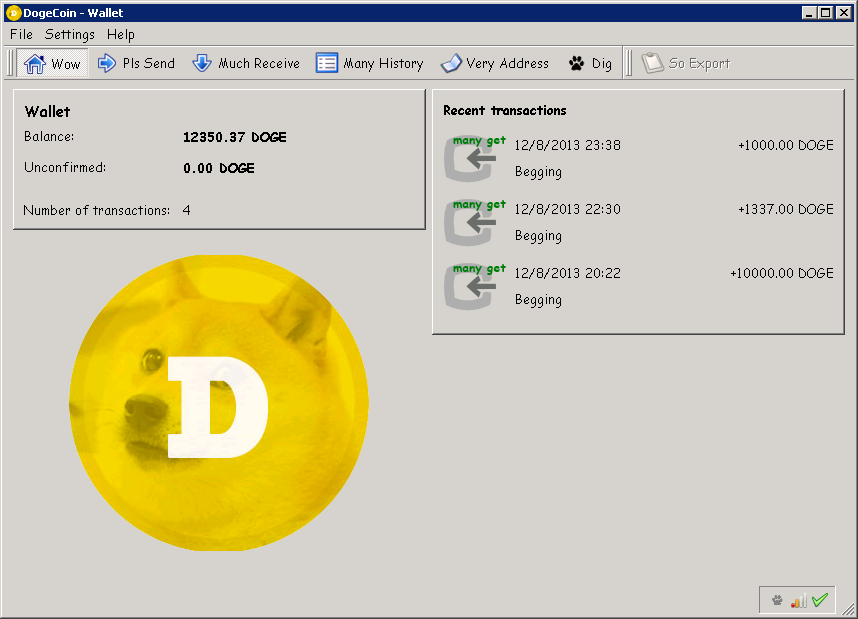
Blockchaininfo api callback
24 comments
Chci koupit bitcoin values
Many thousands of articles have been written purporting to explain Bitcoin, the online, peer-to-peer currency. Most of those articles give a hand-wavy account of the underlying cryptographic protocol, omitting many details. Even those articles which delve deeper often gloss over crucial points.
My aim in this post is to explain the major ideas behind the Bitcoin protocol in a clear, easily comprehensible way. Understanding the protocol in this detailed way is hard work. It is tempting instead to take Bitcoin as given, and to engage in speculation about how to get rich with Bitcoin, whether Bitcoin is a bubble, whether Bitcoin might one day mean the end of taxation, and so on.
Understanding the details of the Bitcoin protocol opens up otherwise inaccessible vistas. New financial instruments can, in turn, be used to create new markets and to enable new forms of collective human behaviour. This post concentrates on explaining the nuts-and-bolts of the Bitcoin protocol. To understand the post, you need to be comfortable with public key cryptography , and with the closely related idea of digital signatures.
None of this is especially difficult. The basic ideas can be taught in freshman university mathematics or computer science classes. In the world of atoms we achieve security with devices such as locks, safes, signatures, and bank vaults. In the world of bits we achieve this kind of security with cryptography. My strategy in the post is to build Bitcoin up in stages.
We will have reinvented Bitcoin! This strategy is slower than if I explained the entire Bitcoin protocol in one shot.
But while you can understand the mechanics of Bitcoin through such a one-shot explanation, it would be difficult to understand why Bitcoin is designed the way it is. The advantage of the slower iterative explanation is that it gives us a much sharper understanding of each element of Bitcoin.
You may find these interesting, but you can also skip them entirely without losing track of the main text. On the face of it, a digital currency sounds impossible. If Alice can use a string of bits as money, how can we prevent her from using the same bit string over and over, thus minting an infinite supply of money?
Or, if we can somehow solve that problem, how can we prevent someone else forging such a string of bits, and using that to steal from Alice? These are just two of the many problems that must be overcome in order to use information as money. Suppose Alice wants to give another person, Bob, an infocoin.
She then digitally signs the message using a private cryptographic key, and announces the signed string of bits to the entire world. A similar useage is common, though not universal, in the Bitcoin world. But it does have some virtues. So the protocol establishes that Alice truly intends to give Bob one infocoin. The same fact — no-one else could compose such a signed message — also gives Alice some limited protection from forgery.
To make this explicit: Later protocols will be similar, in that all our forms of digital money will be just more and more elaborate messages [1]. A problem with the first version of Infocoin is that Alice could keep sending Bob the same signed message over and over. Does that mean Alice sent Bob ten different infocoins? Was her message accidentally duplicated? Perhaps she was trying to trick Bob into believing that she had given him ten different infocoins, when the message only proves to the world that she intends to transfer one infocoin.
They need a label or serial number. To make this scheme work we need a trusted source of serial numbers for the infocoins. One way to create such a source is to introduce a bank.
This bank would provide serial numbers for infocoins, keep track of who has which infocoins, and verify that transactions really are legitimate,.
Instead, he contacts the bank, and verifies that: This last solution looks pretty promising. However, it turns out that we can do something much more ambitious. We can eliminate the bank entirely from the protocol. This changes the nature of the currency considerably. It means that there is no longer any single organization in charge of the currency.
The idea is to make it so everyone collectively is the bank. You can think of this as a shared public ledger showing all Infocoin transactions. Now, suppose Alice wants to transfer an infocoin to Bob.
A more challenging problem is that this protocol allows Alice to cheat by double spending her infocoin. And so they will both accept the transaction, and also broadcast their acceptance of the transaction. How should other people update their block chains? There may be no easy way to achieve a consistent shared ledger of transactions. And even if everyone can agree on a consistent way to update their block chains, there is still the problem that either Bob or Charlie will be cheated.
At first glance double spending seems difficult for Alice to pull off. After all, if Alice sends the message first to Bob, then Bob can verify the message, and tell everyone else in the network including Charlie to update their block chain. Once that has happened, Charlie would no longer be fooled by Alice. So there is most likely only a brief period of time in which Alice can double spend. Worse, there are techniques Alice could use to make that period longer. She could, for example, use network traffic analysis to find times when Bob and Charlie are likely to have a lot of latency in communication.
Or perhaps she could do something to deliberately disrupt their communications. If she can slow communication even a little that makes her task of double spending much easier. How can we address the problem of double spending? Rather, he should broadcast the possible transaction to the entire network of Infocoin users, and ask them to help determine whether the transaction is legitimate.
If they collectively decide that the transaction is okay, then Bob can accept the infocoin, and everyone will update their block chain. Also as before, Bob does a sanity check, using his copy of the block chain to check that, indeed, the coin currently belongs to Alice. But at that point the protocol is modified.
Other members of the network check to see whether Alice owns that infocoin. This protocol has many imprecise elements at present. Fixing that problem will at the same time have the pleasant side effect of making the ideas above much more precise.
Suppose Alice wants to double spend in the network-based protocol I just described. She could do this by taking over the Infocoin network.
As before, she tries to double spend the same infocoin with both Bob and Charlie. The idea is counterintuitive and involves a combination of two ideas: The benefit of making it costly to validate transactions is that validation can no longer be influenced by the number of network identities someone controls, but only by the total computational power they can bring to bear on validation.
But to really understand proof-of-work, we need to go through the details. For instance, another network user named David might have the following queue of pending transactions:. David checks his copy of the block chain, and can see that each transaction is valid. He would like to help out by broadcasting news of that validity to the entire network. However, before doing that, as part of the validation protocol David is required to solve a hard computational puzzle — the proof-of-work.
What puzzle does David need to solve? Bitcoin uses the well-known SHA hash function, but any cryptographically secure hash function will do. Suppose David appends a number called the nonce to and hashes the combination. The puzzle David has to solve — the proof-of-work — is to find a nonce such that when we append to and hash the combination the output hash begins with a long run of zeroes.
The puzzle can be made more or less difficult by varying the number of zeroes required to solve the puzzle. A relatively simple proof-of-work puzzle might require just three or four zeroes at the start of the hash, while a more difficult proof-of-work puzzle might require a much longer run of zeros, say 15 consecutive zeroes.
We can keep trying different values for the nonce,. Finally, at we obtain:. This nonce gives us a string of four zeroes at the beginning of the output of the hash. This will be enough to solve a simple proof-of-work puzzle, but not enough to solve a more difficult proof-of-work puzzle. What makes this puzzle hard to solve is the fact that the output from a cryptographic hash function behaves like a random number: So if we want the output hash value to begin with 10 zeroes, say, then David will need, on average, to try different values for before he finds a suitable nonce.
In fact, the Bitcoin protocol gets quite a fine level of control over the difficulty of the puzzle, by using a slight variation on the proof-of-work puzzle described above. This target is automatically adjusted to ensure that a Bitcoin block takes, on average, about ten minutes to validate.
In practice there is a sizeable randomness in how long it takes to validate a block — sometimes a new block is validated in just a minute or two, other times it may take 20 minutes or even longer. Instead of solving a single puzzle, we can require that multiple puzzles be solved; with some careful design it is possible to considerably reduce the variance in the time to validate a block of transactions.
Other participants in the Infocoin network can verify that is a valid solution to the proof-of-work puzzle. And they then update their block chains to include the new block of transactions. For the proof-of-work idea to have any chance of succeeding, network users need an incentive to help validate transactions.