JK flip-flops up-down counter from 0 to 9
5 stars based on
37 reviews
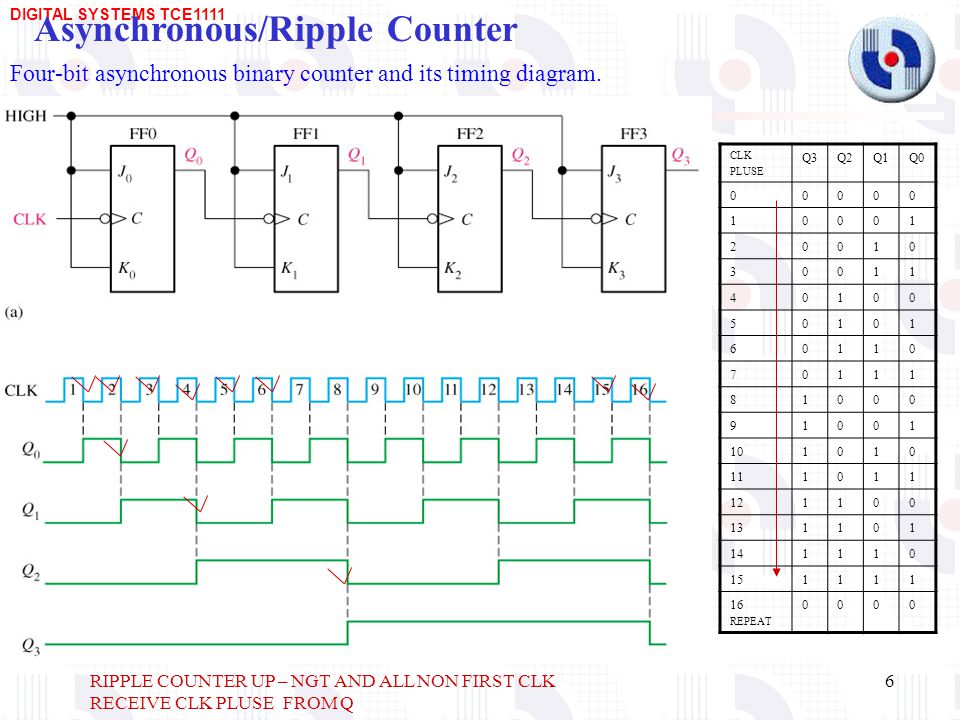
The Web This site. The output is a binary value whose value is equal to the number of pulses received at the CK input. Each output represents one bit of the output word, which, in 74 series counter ICs is usually 4 bits long, and the size of the output word depends on the number of flip-flops that make up the counter.
The output lines of a 4-bit counter represent the values 2 02 12 3 bit ripple counter pdf to jpg and 2 3 3 bit ripple counter pdf to jpg, or 1,2,4 and 8 respectively. They are normally shown in schematic diagrams in reverse order, with the least significant bit at the left, this is to enable the schematic diagram to show the circuit following the convention that signals flow 3 bit ripple counter pdf to jpg left to right, therefore in this case the 3 bit ripple counter pdf to jpg input is at the left.
The rising edge of the Q output of each flip-flop triggers the CK input of the next flip-flop at half the frequency of the CK pulses applied to its input. The Q outputs then represent a four-bit binary count with Q 0 to Q 3 representing 2 0 1 to 2 3 8 respectively. Assuming that the four Q outputs are initially atthe rising edge of the first CK pulse applied will cause the output Q 0 to go to logic 1, and the next CK pulse will make Q 0 output return to logic 0, and at the same time Q 0 will go from 0 to 1.
The next 3 bit ripple counter pdf to jpg CK pulse will cause Q 0 to go to logic 1 again, so both Q 0 and Q 1 will now be high, making the 4-bit output 2 3 10 remembering that Q 0 is the least significant bit. The fourth CK pulse will make both Q 0 and Q 1 return to 0 and as Q 1 will go high at this time, this will toggle FF2, making Q 2 high and indicating 2 4 10 at the outputs.
Reading the output word from right to left, the Q outputs therefore continue to represent a binary number equalling the number of input pulses received at the CK input of FF0.
As this is a four-stage counter the flip-flops will continue to toggle in sequence and the four Q outputs will output a sequence of binary 3 bit ripple counter pdf to jpg from 2 to 2 0 to 15 10 before the output returns to 2 and begins to count up 3 bit ripple counter pdf to jpg as illustrated by the waveforms in Fig 3 bit ripple counter pdf to jpg.
To convert the up 3 bit ripple counter pdf to jpg in Fig. By taking both the output lines and the CK pulse for the next flip-flop in sequence from the Q output as shown in Fig.
Although both up and down counters can be built, using the asynchronous method for propagating the clock, they are not widely used as counters as they become unreliable at high clock speeds, or when a large number of flip-flops are connected together to give larger counts, due to the clock ripple effect. The effect of clock ripple in asynchronous counters is illustrated in Fig. As the Q 0 to Q 3 outputs each change at different times, a number of different output states occur as any particular clock pulse causes a new value to appear 3 bit ripple counter pdf to jpg the outputs.
At CK pulse 8 for example, the outputs Q 0 to Q 3 should change from 2 7 10 to 2 8 10however what really happens reading the vertical columns 3 bit ripple counter pdf to jpg 1s and 0s in Fig.
At CK pulses other that pulse 8 of course, different sequences will occur, therefore there will be periods, as a change of value ripples through the chain of flip-flops, when unexpected values appear at the Q outputs for a very short time.
However this can cause problems when a particular binary value is to be selected, as in the case of a decade counter, which must count from 2 to 2 9 10 and then reset to 2 on a count of 2 10 These short-lived logic values will also cause a series of very short spikes on the Q outputs, as the propagation delay of a single flip-flop is only about to ns.
Although this problem prevents the circuit being used as a reliable counter, it is still valuable as a simple and effective 3 bit ripple counter pdf to jpg divider, where a high frequency oscillator provides the input and each flip-flop in the chain divides the frequency by two.
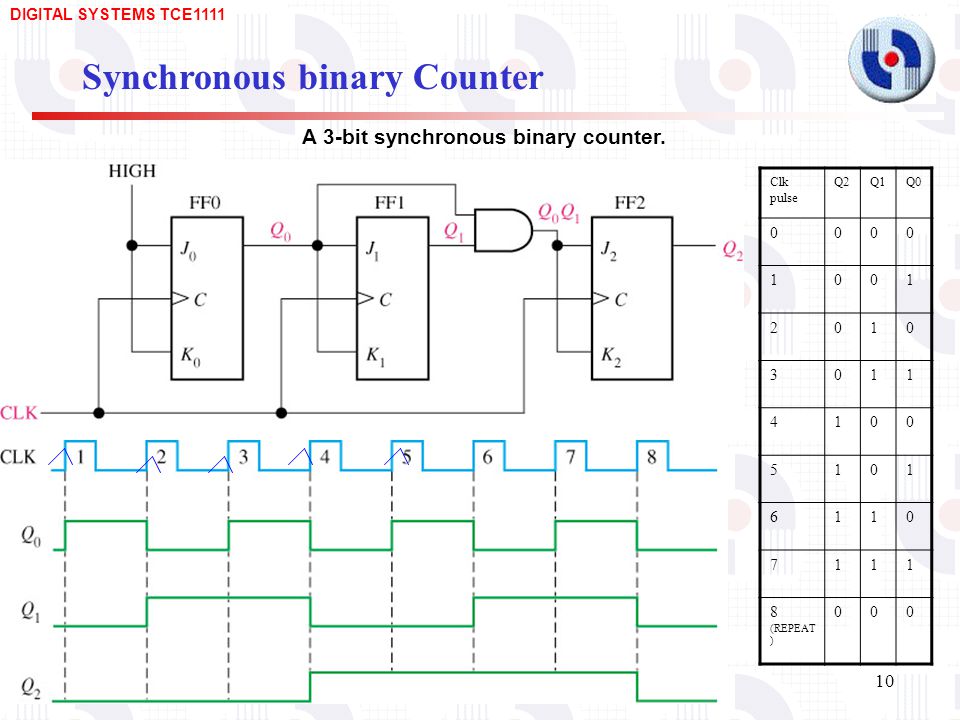
The synchronous counter provides a more reliable circuit for counting purposes, and for high-speed operation, as the clock pulses in this circuit are fed to every flip-flop in the chain at exactly the same time. Synchronous counters use JK flip-flops, as the programmable J and K inputs allow the toggling of individual flip-flops to be enabled or disabled at various stages of the count. Synchronous counters therefore eliminate the clock ripple problem, as the operation of the circuit is synchronised to the CK pulses, rather than flip-flop outputs.
Notice that the CK input is applied to all the flip-flops in parallel. Therefore, as all the flip-flops receive a clock pulse at the same instant, some method must be used to prevent all the flip-flops changing state at the same time.
This of course would result in the counter outputs simply toggling from all ones to all zeros, and back again with each clock pulse. However, with JK flip-flops, when both J and K inputs are logic 1 the output toggles on each CK pulse, but when J and K are both at logic 0 no change takes place.
The binary output is taken from the Q outputs of the flip-flops. Note that on FF0 the J and K inputs are permanently wired to logic 1, so Q 0 will change state toggle on each clock pulse. In adding a third flip flop to the counter however, direct connection from J and K to the previous Q 1 output would not give the correct count. Because Q 1 is high at a count of 2 10 this would mean that FF2 would toggle on clock pulse three, as J2 and K2 would be high.
Therefore clock pulse 3 would give a binary count of 2 or 7 10 instead of 4 To prevent this problem an AND gate is used, 3 bit ripple counter pdf to jpg shown 3 bit ripple counter pdf to jpg Fig.
Only when the outputs are in this state will the next clock pulse toggle Q 2 to logic 1. The outputs Q 0 and Q 1 will of course return to logic 0 on this pulse, so giving a count of 2 or 4 10 with Q 0 being the least significant bit. Q 3 therefore will not toggle to its high state until the eighth clock pulse, and will remain high until the sixteenth 3 bit ripple counter pdf to jpg pulse. After this pulse, all the Q outputs will return to zero.
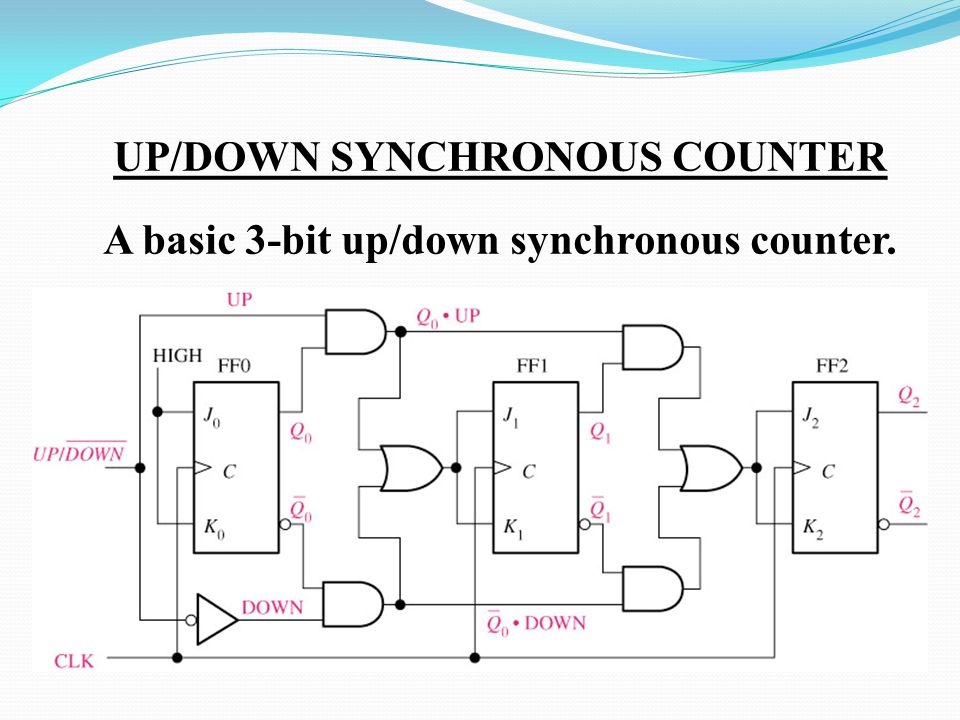
Note that for this basic form of the synchronous counter to work, the PR and CLR inputs must also be all at logic 1, their inactive state as shown in Fig. Converting the synchronous up counter to count down is simply a matter of reversing the count. If all of the ones and zeros in the 0 to 15 10 sequence shown in Table 5. As every Q output on the JK flip-flops has its complement on Qall that is needed to convert the up counter in Fig.
Each group of gates between successive flip-flops is in fact a modified data select circuit described in Combinational Logic Module 4. This is necessary to provide the correct logic state for the next data selector. If the control input is at logic 1 then the CK pulse to the next flip-flop is fed from the Q output, making the counter an UP counter, but if the control input is 0 then CK pulses are fed from Q and the counter is a DOWN counter.
When Q 1 and Q 3 are both at logic 1, the output terminal of the limit detection NAND gate LD1 will become logic 0 and reset all the flip-flop outputs to logic 0. Because the first time Q 1 and Q 3 are both at logic 1 during a 0 to 15 10 count is at a count of ten 2this will cause the counter to count from 0 to 9 10 and then reset to 0, omitting 10 10 to 15 The circuit is therefore a BCD counter, an extremely useful device for driving numeric displays via a BCD to 7-segment decoder etc.
However by re-designing the gating system to produce logic 0 at the 3 bit ripple counter pdf to jpg inputs for a different maximum value, any count other than 0 to 15 can be achieved. If you already have a simulator such as Logisim installed on your computer, why not try designing an Octal up counter for example.
Although synchronous counters can be, and are built from individual JK flip-flops, in many circuits they will be ether built into dedicated counter ICs, or into other large scale integrated circuits LSICs. For many applications the counters contained within ICs have extra inputs and outputs added to increase the counters versatility.
The differences between many commercial counter ICs are basically the different input and output facilities offered. Some of which are described below. Notice that many of these inputs are active low; this derives from the fact that in earlier TTL devices any unconnected input would float up to logic 1 and hence become inactive. However leaving inputs un-connected is not good practice, especially CMOS inputs, which float between logic states, and could easily be activated to either valid logic state by random noise in the circuit, therefore ANY unused input should be permanently connected to its inactive logic state.
Count Enable CTEN for 3 bit ripple counter pdf to jpg, is a feature on counter integrated circuits, and in the synchronous counter illustrated in Fig 5.
When it is set to logic 1, it will prevent the count from progressing, even in the presence of clock pulses, but the count will continue normally when CTEN 3 bit ripple counter pdf to jpg at logic 0. A common way of disabling the counter, whilst retaining any current data on the Q outputs, is to inhibit the toggle action of the JK flip-flops whilst CTEN is inactive logic 1by making the JK inputs of all the flip-flops logic 0.
When the count is disabled, CTEN and therefore one of the inputs on each ofE1, E2 and E3 will be at logic 0, which will cause these enable gate outputs, and the flip-flop JK inputs to also be at logic 0, whatever logic states are present on the Q outputs, and also at the other enable gate inputs. Therefore whenever CTEN is at logic 1 the count is disabled. In this condition, when the next clock pulse is received at the CK input the flip-flops will toggle, following their normal sequence.
Using a separate DATA input for each flip-flop, and a small amount of extra logic, a logic 0 on the PL will load the counter with any pre-determined binary value before the 3 bit ripple counter pdf to jpg of, or during the count. A method of achieving asynchronous parallel loading on a synchronous counter is shown in Fig.
The binary value to be loaded into the counter is applied to inputs D 0 to D 3 and a logic 0 pulse is applied to the PL input. This logic 0 is inverted and applied to one input of each of the eight NAND gates to enable them.
If the value to be loaded into a particular flip-flop is logic 1, this makes the inputs of the right hand NAND gate 1,1 and due to 3 bit ripple counter pdf to jpg inverter between the pair of NAND gates for that particular input, the left hand NAND gate inputs will be 1,0. The result of this is that logic 0 is applied to the flip-flop PR input and logic 1 is applied to the CLR input.
This combination sets the Q output to logic 1, the same value that was applied to the D input. Similarly if a D input is at logic 0 the output of the left hand NAND gate of the pair will be Logic 0 and the right hand gate output will be logic 1, which will clear the Q output 3 bit ripple counter pdf to jpg the flip-flop.
Because the PL input is common to each pair of load NAND gates, all four flip-flops are loaded simultaneously with the value, either 1 or 0 present at its particular D input. Modifications such 3 bit ripple counter pdf to jpg those described in this module make the basic synchronous counter much more versatile. Both TTL and CMOS synchronous counters are available in the 74 series of ICs containing usually 4-bit counters with these and other modifications for a wide variety of applications.
Stops count without resetting when at logic 1. TC can be used to detect the end of an up or down count, and as well as being available as an output, TC is used internally to generate the Ripple Carry output. Connecting Synchronous counters in cascade, to obtain greater count ranges, is made simple in ICs such as the 74HC by using the ripple carry RC output of the IC counting the least significant 4 bits, to drive the clock input of the next most significant IC, as show in red in Fig.
Although it may appear that either the TC or the RC outputs could drive the next clock input, the TC output is not intended for this purpose, as timing issues can occur. Although synchronous counters have a great advantage over asynchronous or ripple counters in regard to reducing timing problems, there are situations where ripple counters have an advantage over synchronous counters.
When used at high speeds, only the first flip-flop in the ripple counter chain runs at the clock frequency. Each subsequent flip-flop runs at half the frequency of the previous one. In synchronous counters, with every stage operating at very high clock frequencies, stray capacitive coupling between the counter and other components and within the counter itself is more likely occur, so that in synchronous counters interference can be transferred between different stages of the counter, upsetting the count if adequate decoupling is not provided.
This problem is reduced in ripple counters due to the lower frequencies in most of the stages. Also, because the clock pulses applied to synchronous counters must charge, and discharge the input capacitance of every flip-flop simultaneously; synchronous counters having many flip-flops will cause large pulses of charge and discharge current in the clock driver circuits every time the clock changes logic state.
This can also cause unwelcome spikes on the supply lines that could cause problems elsewhere in the digital circuitry. This is less of a problem with asynchronous counters, as the clock is only driving the first flip-flop in the counter chain. Asynchronous counters are mostly used for frequency division applications and for generating time delays. In either of these applications the timing of individual outputs is not likely to cause a problem to external circuitry, and the fact that most of the stages in the counter run at much lower frequencies than the input clock, greatly reduces any problem of high frequency noise interference to surrounding components.
Hons All rights reserved. Learn about electronics Digital Electronics. After studying this section, you should be able to: Understand the operation of digital counter circuits and can: Describe the action of asynchronous ripple counters using D Type flip flops. Understand the operation of synchronous counters.
Describe common control features used in synchronous counters. Use software to simulate counter operation.